Reliability of Factor Scores

Yixiao Li, Winnie Tse, Mark Lai

2024-09-06

In this vignette, we explore analytically the reliability of factor scores, and evaluate them using simulated data.

library(lavaan)

## This is lavaan 0.6-18
## lavaan is FREE software! Please report any bugs.

library(R2spa)
library(tidyr)
library(ggplot2)

Analytic Formula for Factor Scores

Theoretical Values

aka, using true parameter values to compute weights

From a unidimensional factor model $\boldsymbol{\mathbf{y}}= \boldsymbol{\mathbf{\lambda }}\eta + \boldsymbol{\mathbf{e}}$, for factor scores of the form

$$\begin{aligned} \tilde \eta & = \boldsymbol{\mathbf{a}}' (\boldsymbol{\mathbf{y}} - \hat {\boldsymbol{\mathbf{\mu}}}) = \boldsymbol{\mathbf{a}}' (\boldsymbol{\mathbf{\nu }}+ \boldsymbol{\mathbf{\lambda }}\eta + \boldsymbol{\mathbf{e}} - \boldsymbol{\mathbf{\nu}}) \\ & = \boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\lambda }}\eta + \boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{e}}, \end{aligned}$$

where we set $\mathop{\mathrm{\mathrm{E}}}(\eta)$ = 0 so that $\hat {\boldsymbol{\mathbf{\mu}}}$ = $\boldsymbol{\mathbf{\nu}}$, the theoretical reliability formula of factor scores, assuming no sampling errors in the weights is given by

$$\rho = \frac{(\boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\lambda}})^2}{(\boldsymbol{\mathbf{a}}'\boldsymbol{\mathbf{\lambda}})^2 + \boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\Theta }}\boldsymbol{\mathbf{a}}},$$

assuming that we set $\mathop{\mathrm{\mathrm{Var}}}(\eta) = 1$.

Regression factor scores

With $\boldsymbol{\mathbf{a}}$ = $(\boldsymbol{\mathbf{\Sigma}}^{-1} \boldsymbol{\mathbf{\lambda}})$,

$$\begin{align*} \text{Rel} &= \frac{(\boldsymbol{\mathbf{\lambda}}' \boldsymbol{\mathbf{\Sigma}}^{-1} \boldsymbol{\mathbf{\lambda}})^2}{\boldsymbol{\mathbf{\lambda}}'\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\lambda }}\boldsymbol{\mathbf{\lambda }}\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\lambda }}+ \boldsymbol{\mathbf{\lambda}}'\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\Theta }}\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\lambda}}} \\ &= \frac{(\boldsymbol{\mathbf{\lambda}}'\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\lambda}})^2}{\boldsymbol{\mathbf{\lambda}}'\boldsymbol{\mathbf{\Sigma}}^{-1}(\boldsymbol{\mathbf{\lambda}}\boldsymbol{\mathbf{\lambda}}'+\boldsymbol{\mathbf{\Theta}})\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\lambda}}} \\ &= \frac{(\boldsymbol{\mathbf{\lambda}}'\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\lambda}})^2}{\boldsymbol{\mathbf{\lambda}}'\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\lambda}}} \\ &= \boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\lambda}} \end{align*}$$

Bartlett factor scores

With $\boldsymbol{\mathbf{a}}$ = $\boldsymbol{\mathbf{\Theta}}^{-1} \boldsymbol{\mathbf{\lambda }}(\boldsymbol{\mathbf{\lambda}}' \boldsymbol{\mathbf{\Theta}}^{-1} \boldsymbol{\mathbf{\lambda}})^{-1}$, and thus $\boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\lambda }}= 1$,

$$\begin{align*} \text{Rel} &= \frac{1}{1 + (\boldsymbol{\mathbf{\lambda}}' \boldsymbol{\mathbf{\Theta}}^{-1} \boldsymbol{\mathbf{\lambda}})^{-1} \boldsymbol{\mathbf{\lambda}}' \boldsymbol{\mathbf{\Theta}}^{-1} \boldsymbol{\mathbf{\Theta }}\boldsymbol{\mathbf{\Theta}}^{-1} \boldsymbol{\mathbf{\lambda }}(\boldsymbol{\mathbf{\lambda}}' \boldsymbol{\mathbf{\Theta}}^{-1} \boldsymbol{\mathbf{\lambda}})^{-1}} \\ &= \frac{1}{1 + (\boldsymbol{\mathbf{\lambda}}' \boldsymbol{\mathbf{\Theta}}^{-1} \boldsymbol{\mathbf{\lambda}})^{-1}} \end{align*}$$

Sample Estimators

When factor scores are computed using sample estimates of $\boldsymbol{\mathbf{\lambda}}$ and $\boldsymbol{\mathbf{\Theta}}$, we have $\hat{\boldsymbol{\mathbf{\mu}}}$ = $\hat{\boldsymbol{\mathbf{\nu}}}$, and

$$\begin{aligned} \tilde \eta & = \hat{\boldsymbol{\mathbf{a}}}' (\boldsymbol{\mathbf{y}} - \hat {\boldsymbol{\mathbf{\mu}}}) = \hat{\boldsymbol{\mathbf{a}}}' (\boldsymbol{\mathbf{\nu }}+ \boldsymbol{\mathbf{\lambda }}\eta + \boldsymbol{\mathbf{e}} - \hat{\boldsymbol{\mathbf{\nu}}}) \\ & = \hat{\boldsymbol{\mathbf{a}}}' \boldsymbol{\mathbf{\lambda }}\eta + \hat{\boldsymbol{\mathbf{a}}}'(\boldsymbol{\mathbf{\nu }}- \hat{\boldsymbol{\mathbf{\nu}}}) + \hat{\boldsymbol{\mathbf{a}}}' \boldsymbol{\mathbf{e}}, \end{aligned}$$

where

• $\boldsymbol{\mathbf{\hat a}}$ = vector of estimated weights of length $p$
• $\boldsymbol{\mathbf{a}}$ = vector of true weights of length $p$,
• $\boldsymbol{\mathbf{y}}$ = vector of observed scores of length $p$,
• $\lambda$ = vector of factor loadings of length $p$,
• $\eta$ = latent variable,
• $\boldsymbol{\mathbf{e}}$ = vector of measurement errors of length $p$,
• $\Theta$ = $\mathop{\mathrm{\mathrm{Var}}}(\boldsymbol{\mathbf{e}})$ = $p \times p$ variance-covariance matrix of errors,
• $p$ = number of items.

If we assume that $\hat{\boldsymbol{\mathbf{a}}}$ and $\hat{\boldsymbol{\mathbf{\nu}}}$ are independent, and $E(\hat{\boldsymbol{\mathbf{a}}}) = \boldsymbol{\mathbf{a}}$, $\mathop{\mathrm{\mathrm{Var}}}(\hat{\boldsymbol{\mathbf{a}}}) = V_{\hat a}$, $E(\hat{\boldsymbol{\mathbf{\nu}}}) = \boldsymbol{\mathbf{\nu}}$, $\mathop{\mathrm{\mathrm{Var}}}(\hat{\boldsymbol{\mathbf{\nu}}}) = V_{\hat \nu}$, then using law of total variance,

$$\begin{aligned} \mathop{\mathrm{\mathrm{Var}}}(\tilde \eta) & = \mathop{\mathrm{\mathrm{E}}}[\mathop{\mathrm{\mathrm{Var}}}(\tilde \eta | \hat{\boldsymbol{\mathbf{a}}})] + \mathop{\mathrm{\mathrm{Var}}}[\mathop{\mathrm{\mathrm{E}}}(\tilde \eta | \hat{\boldsymbol{\mathbf{a}}})] \\ & = \mathop{\mathrm{\mathrm{E}}}[\hat {\boldsymbol{\mathbf{a}}}' \boldsymbol{\mathbf{\lambda }}\boldsymbol{\mathbf{\lambda}}' \hat{\boldsymbol{\mathbf{a}}} + \boldsymbol{\mathbf{a}}' V_{\hat \nu} \boldsymbol{\mathbf{a}} + \hat {\boldsymbol{\mathbf{a}}}' \boldsymbol{\mathbf{\Theta }}\hat{\boldsymbol{\mathbf{a}}}] + V[\hat{\boldsymbol{\mathbf{a}}}' 0] \\ & = \boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\lambda }}\boldsymbol{\mathbf{\lambda}}' \boldsymbol{\mathbf{a}} + \mathop{\mathrm{\mathrm{Tr}}}(V_{\hat a} \boldsymbol{\mathbf{\lambda }}\boldsymbol{\mathbf{\lambda}}') + \boldsymbol{\mathbf{a}}' V_{\hat \nu} \boldsymbol{\mathbf{a}} + \mathop{\mathrm{\mathrm{Tr}}}(V_{\hat a} V_{\hat \nu}) + \boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\Theta }}\boldsymbol{\mathbf{a}} + \mathop{\mathrm{\mathrm{Tr}}}(V_{\hat a} \boldsymbol{\mathbf{\Theta}}) \end{aligned}$$

So, accounting for sampling error,

$$\rho = \frac{(\boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\lambda}})^2 + \boldsymbol{\mathbf{\lambda}}'V_{\hat a} \boldsymbol{\mathbf{\lambda}}}{(\boldsymbol{\mathbf{a}}' \boldsymbol{\mathbf{\lambda}})^2 + \boldsymbol{\mathbf{a}}'\boldsymbol{\mathbf{\Theta }}\boldsymbol{\mathbf{a}} + \boldsymbol{\mathbf{\lambda}}'V_{\hat a}\boldsymbol{\mathbf{\lambda }}+ \boldsymbol{\mathbf{a}}' V_{\hat \nu} \boldsymbol{\mathbf{a}} + \mathop{\mathrm{\mathrm{Tr}}}(V_{\hat a} V_{\hat \nu}) + \mathop{\mathrm{\mathrm{Tr}}}(\boldsymbol{\mathbf{\Theta }}\boldsymbol{\mathbf{V}}_{\hat a})}$$

The sample estimates can be obtained by substituting in the sample estimates of $\boldsymbol{\mathbf{\lambda}}$ and $\boldsymbol{\mathbf{\Theta}}$ and using the corresponding form of $\boldsymbol{\mathbf{a}}$.

Quadratic formula for regression factor scores

The reliability formula for the regression factor scores derived using a quadratic formula is

$$\text{Rel} = \frac{1\pm\sqrt{1 - 4\theta_{corrected}/\psi}}{2}$$

where $\theta_{corrected}$ is the corrected error term for the factor scores.

Empirical Example

Regression Factor Scores

# Three items from the classic Holzinger and Swineford (1939) data
cfa_fit <- cfa("
  visual =~ x1 + x2 + x3
",
  data = HolzingerSwineford1939,
  std.lv = TRUE
)
# Uncorrected reliability of regression factor scores
fsr <- lavPredict(cfa_fit, fsm = TRUE, acov = TRUE)
attr(fsr, "fsm")[[1]] %*% lavInspect(cfa_fit, what = "est")$lambda

##           visual
## visual 0.6598382

# Empirical reliability of regression factor scores
var(fsr) / (var(fsr) + attr(fsr, "acov")[[1]])

##           visual
## visual 0.6605848

# Corrected reliability of regression factor scores
get_a <- function(lambda, theta) {
  solve(tcrossprod(lambda) + theta, lambda)
}
lam <- lavInspect(cfa_fit, what = "est")$lambda
th <- lavInspect(cfa_fit, what = "est")$theta
jac_a <- lavaan::lav_func_jacobian_complex(
  \(x) get_a(x[1:3], diag(x[4:6])),
  x = c(lam, diag(th))
)
# Estimated sampling variance of weights
va <- jac_a %*% vcov(cfa_fit)[1:6, 1:6] %*% t(jac_a)
aa <- tcrossprod(get_a(lam, th)) + va
sum(diag(tcrossprod(lam) %*% aa)) /
  sum(diag(cfa_fit@implied$cov[[1]] %*% aa))

## [1] 0.64774

# Or using `get_fs_lavaan`
get_fs_lavaan(cfa_fit, reliability = TRUE) |>
  attr(which = "reliability")

## [1] 0.64774

Bartlett Factor Scores

# Uncorrected reliability of Bartlett factor scores
fsb <- lavPredict(cfa_fit, method = "Bartlett", fsm = TRUE, acov = TRUE)
1 / (1 + attr(fsb, "acov")[[1]])

##           visual
## visual 0.6598382

# Empirical reliability of regression factor scores
(var(fsb) - attr(fsb, "acov")[[1]]) / var(fsb)

##           visual
## visual 0.6609684

# Corrected reliability of regression factor scores
get_a <- function(lambda, theta) {
  thinv_lam <- solve(theta, lambda)
  solve(crossprod(lambda, thinv_lam), t(thinv_lam))
}
lam <- lavInspect(cfa_fit, what = "est")$lambda
th <- lavInspect(cfa_fit, what = "est")$theta
jac_a <- lavaan::lav_func_jacobian_complex(
  \(x) get_a(x[1:3], diag(x[4:6])),
  x = c(lam, diag(th))
)
# Estimated sampling variance of weights
va <- jac_a %*% vcov(cfa_fit)[1:6, 1:6] %*% t(jac_a)
aa <- tcrossprod(t(get_a(lam, th))) + va
sum(diag(tcrossprod(lam) %*% aa)) /
  sum(diag(cfa_fit@implied$cov[[1]] %*% aa))

## [1] 0.6477805

# Or using `get_fs_lavaan` (need to be fixed)
R2spa::get_fs_lavaan(cfa_fit, method = "Bartlett", reliability = TRUE) |>
  attr(which = "reliability")

## [1] 0.6477805

Multiple-group example

mod <- "
  visual =~ x1 + x2 + x3
"
get_fs(HolzingerSwineford1939, model = mod, group = "school",
       reliability = TRUE, std.lv = TRUE, method = "regression") |>
  attr(which = "reliability")

## $Pasteur
## [1] 0.6473336
## 
## $`Grant-White`
## [1] 0.6789831
## 
## $overall
## [1] 0.66258

get_fs(HolzingerSwineford1939, model = mod, group = "school",
       reliability = TRUE, std.lv = TRUE, method = "Bartlett") |>
  attr(which = "reliability")

## $Pasteur
## [1] 0.6474885
## 
## $`Grant-White`
## [1] 0.6790979
## 
## $overall
## [1] 0.6627156

Simulations

set.seed(2356)
lambda <- seq(.3, .9, length.out = 6)
theta <- 1 - lambda^2
num_obs <- 100

num_sims <- 2000
out <- matrix(ncol = 7, nrow = num_sims)

# Copy function for computing a
get_a <- function(lambda, theta) {
  solve(tcrossprod(lambda) + theta, lambda)
}

# Function for getting all versions
all_rel <- function(lam, th, vc) {
  sigma <- tcrossprod(lam) + th
  ahat <- crossprod(lam, solve(sigma))
  # Formula 1: no adjustment
  rel1 <- ahat %*% lam

  jac_a <- lavaan::lav_func_jacobian_complex(
    function(x, p) {
      get_a(x[seq_len(p)], theta = diag(x[-(seq_len(p))]))
    },
    x = c(lam, diag(th)),
    p = length(lam)
  )
  va <- jac_a %*% vc %*% t(jac_a)
  aa <- crossprod(ahat) + va
  # Formula 2: adjust for both error in weights and true variances
  rel2 <- sum(diag(tcrossprod(lam) %*% aa)) / sum(diag(sigma %*% aa))

  ev_fs <- sum(diag(th %*% aa))
  # Formula 3: solve quadratic equation with adjusted error
  rel3 <- (1 + sqrt(1 - 4 * ev_fs)) / 2

  c(rel1, rel2, rel3)
}

# Function for getting all bias-corrected versions
all_bc_rel <- function(fit, nsim = 500) {
  vc <- vcov(fit)
  mc_sim <- MASS::mvrnorm(nsim, mu = coef(fit), Sigma = vc)
  mc_rel <- apply(mc_sim, MARGIN = 1,
                  FUN = function(x) {
                    all_rel(x[1:6], th = diag(x[7:12]), vc = vc)
                  })
  2 * with(
    lavInspect(fit, what = "est"),
    all_rel(lambda, th = theta, vc = vc)
  ) - rowMeans(mc_rel) # bias-corrected
}

for (i in seq_len(num_sims)) {
  eta <- rnorm(num_obs)
  err <- matrix(
    rnorm(num_obs * length(lambda), sd = sqrt(theta)),
    ncol = num_obs
  )
  y <- t(
    tcrossprod(lambda, eta) + err
  )
  # Run cfa
  fit <- cfa("f =~ y1 + y2 + y3 + y4 + y5 + y6",
    data = data.frame(y) |> setNames(paste0("y", seq_along(lambda))),
    std.lv = TRUE
  )
  pars_fit <- lavInspect(fit, what = "est")
  tilde_eta <- lavPredict(fit, fsm = TRUE)
  true_rel <- cor(tilde_eta, eta)^2
  est_a <- attr(tilde_eta, "fsm")[[1]]
  out[i, ] <- c(
    true_rel,
    all_rel(pars_fit$lambda, pars_fit$theta, vcov(fit)),
    all_bc_rel(fit)
  )
  setTxtProgressBar(
    txtProgressBar(min = 0, max = num_sims, style = 3, width = 50, char = "="), 
    i
  )
}
colnames(out) <- c("true_rel", "no_adj_rel", "adj_rel", "quadratic",
                   "no_adj_rel_bc", "adj_rel_bc", "quadratic_bc")

# save the file
saveRDS(out, "vignettes/sim_results_reliability.RDS")

# Mean bias
out <- readRDS("sim_results_reliability.RDS")
data.frame(
  Type = c("no_adj_rel", "adj_rel", "quadratic",
           "no_adj_rel_bc", "adj_rel_bc", "quadratic_bc"),
  Raw_Biases = c(mean(out[, "no_adj_rel"] - out[, "true_rel"]), 
                 mean(out[, "adj_rel"] - out[, "true_rel"]), 
                 mean(out[, "quadratic"] - out[, "true_rel"]), 
                 mean(out[, "no_adj_rel_bc"] - out[, "true_rel"]), 
                 mean(out[, "adj_rel_bc"] - out[, "true_rel"]), 
                 mean(out[, "quadratic_bc"] - out[, "true_rel"], na.rm = TRUE))
) |>
  knitr::kable(digits = 3)

Type	Raw_Biases
no_adj_rel	0.019
adj_rel	0.011
quadratic	0.008
no_adj_rel_bc	0.012
adj_rel_bc	0.005
quadratic_bc	0.001

# RMSE: 
data.frame(
  Type = c("no_adj_rel", "adj_rel", "quadratic",
           "no_adj_rel_bc", "adj_rel_bc", "quadratic_bc"),
  RMSE = c(sqrt(mean((out[, "no_adj_rel"] - out[, "true_rel"])^2)),
           sqrt(mean((out[, "adj_rel"] - out[, "true_rel"])^2)),
           sqrt(mean((out[, "quadratic"] - out[, "true_rel"])^2)),
           sqrt(mean((out[, "no_adj_rel_bc"] - out[, "true_rel"])^2)),
           sqrt(mean((out[, "adj_rel_bc"] - out[, "true_rel"])^2)),
           sqrt(mean((out[, "quadratic_bc"] - out[, "true_rel"])^2, 
                     na.rm = TRUE)))
) |>
  knitr::kable(digits = 3)

Type	RMSE
no_adj_rel	0.046
adj_rel	0.042
quadratic	0.042
no_adj_rel_bc	0.042
adj_rel_bc	0.040
quadratic_bc	0.040

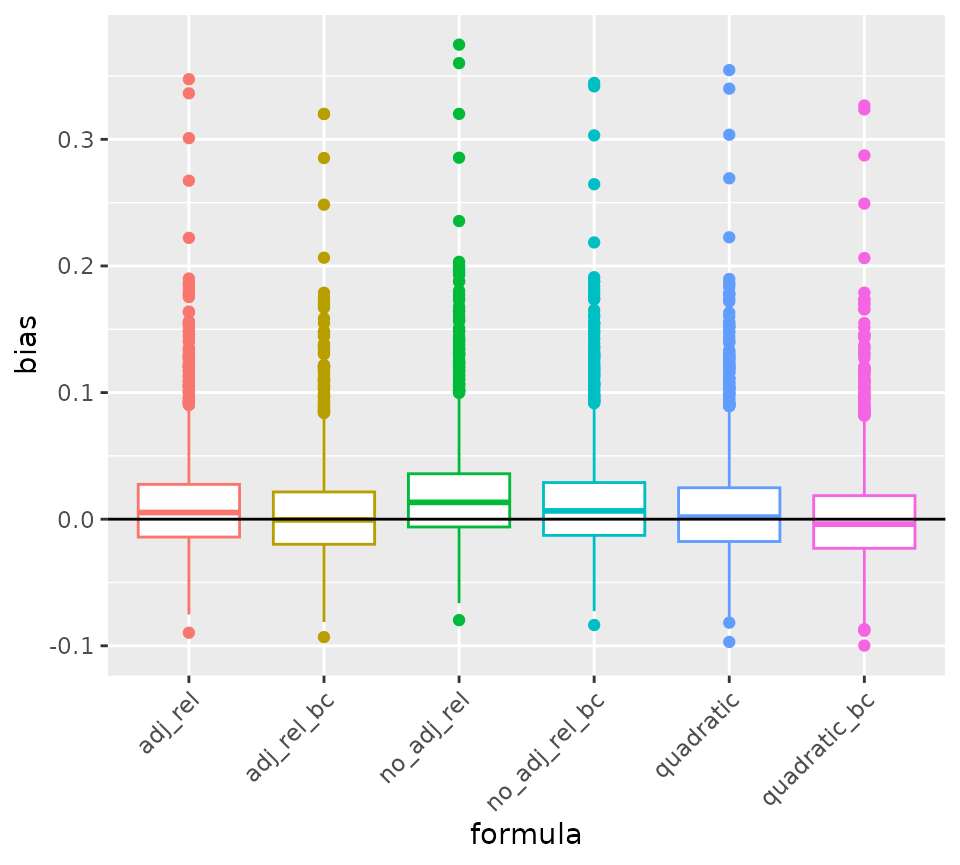
# Boxplot to compare the bias across formula
bias_tab <- as.data.frame(out[, -1] - out[, 1]) |>
  pivot_longer(everything(), names_to = "formula", values_to = "bias")
bias_tab |>
  ggplot(aes(x = formula, y = bias, col = formula)) +
  geom_boxplot() +
  geom_hline(yintercept = 0) +
  theme(legend.position = "none",
        axis.text.x = element_text(angle = 45, hjust = 1))

## Warning: Removed 6 rows containing non-finite outside the scale range
## (`stat_boxplot()`).